Sunspot activity and influenza pandemics assessment by Cambridge university
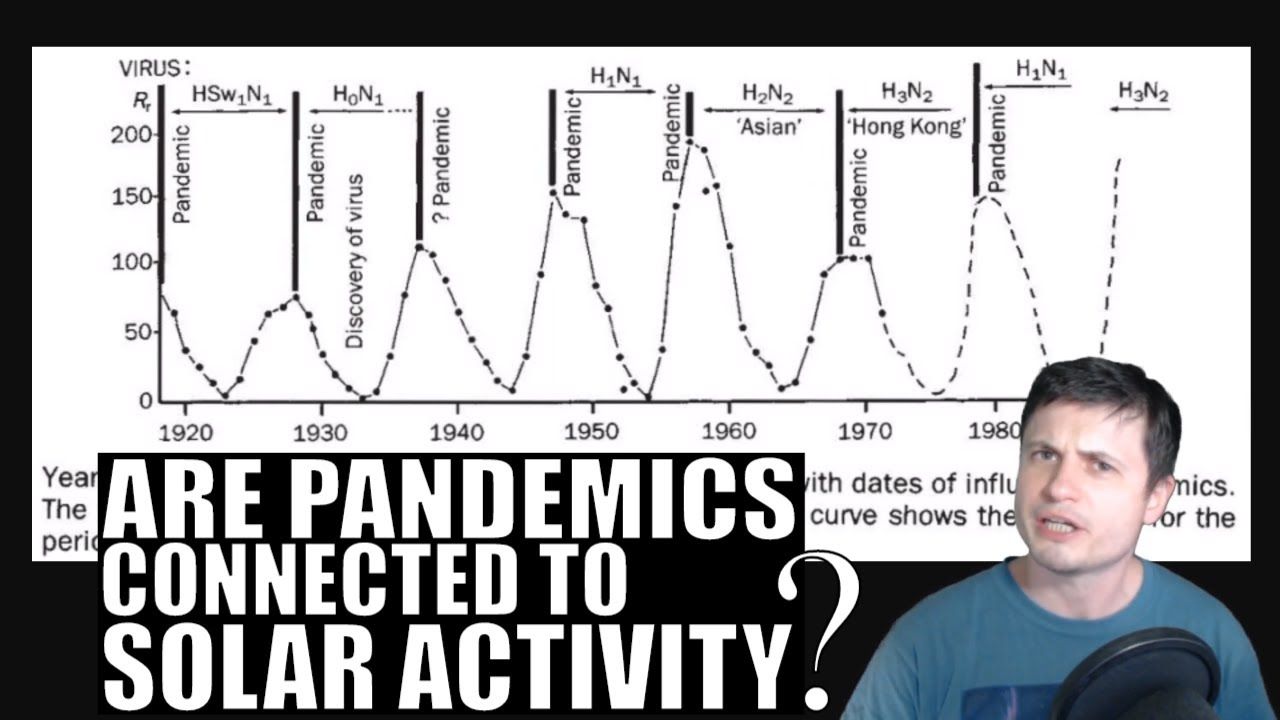
A statistical assessment of the purported association between sunspot activity and influenza pandemics.
- Published online by Cambridge University Press: 29 August 2017
When the mis-transcribed data in several of the following presentations were corrected and several derivative sources were removed, this analysis found no statistically significant difference between the distribution of Q for pandemic years compared with other years.
Summary
Since 1978, a series of papers in the literature have claimed to find a significant association between sunspot activity and the timing of influenza pandemics. This paper examines these analyses, and attempts to recreate the three most recent statistical analyses by Ertel (1994), Tapping et al. (2001), and Yeung (2006), which all have purported to find a significant relationship between sunspot numbers and pandemic influenza. As will be discussed, each analysis had errors in the data. In addition, in each analysis arbitrary selections or assumptions were also made, and the authors did not assess the robustness of their analyses to changes in those arbitrary assumptions. Varying the arbitrary assumptions to other, equally valid, assumptions negates the claims of significance.
Indeed, an arbitrary selection made in one of the analyses appears to have resulted in almost maximal apparent significance; changing it only slightly yields a null result. This analysis applies statistically rigorous methodology to examine the purported sunspot/pandemic link, using more statistically powerful un-binned analysis methods, rather than relying on arbitrarily binned data. The analyses are repeated using both the Wolf and Group sunspot numbers. In all cases, no statistically significant evidence of any association was found. However, while the focus in this particular analysis was on the purported relationship of influenza pandemics to sunspot activity, the faults found in the past analyses are common pitfalls; inattention to analysis reproducibility and robustness assessment are common problems in the sciences, that are unfortunately not noted often enough in review.
INTRODUCTION
Influenza pandemics have occurred at irregular intervals throughout human history, causing widespread morbidity and mortality. Pandemic influenza viruses are known to be re-assorted human/animal strains of the virus to which humans have little prior immunity, but the mechanisms are poorly understood that make one re-assorted strain cause a pandemic, while countless others do not ref. [1].
The paper that first claimed a connection between solar activity and influenza was published by Hope-Simpson in 1978 [2]. Hope-Simpson long espoused the view that influenza is not a contagious disease, but rather associated with human responses to solar phenomenon [3]. His 1978 paper purported, without any reference to literature to support the claim, that six influenza ‘pandemics’ occurred between 1918 and 1971, and the timing of each were all within ±1 year of a maximum in the sunspot cycle.
However, in reality, only three pandemics are generally agreed upon to have occurred during that time period [4–13]. It is true that of these three (1918, 1957, and 1968), all in fact occurred within ±1 year of the solar cycle peaks. However, a trivial statistical analysis shows that this is not extraordinary; the Binomial 95% confidence interval for the estimated probability of observing a pandemic within ±1 year of a peak when three out of three have actually been observed is [0·29, 1·0] [14], but of all years during that time period, 16 out of 54 (30%) were within ±1 year of peak. This null hypothesis value of 30% is at the lower end of the Binomial 95% confidence interval of the observed, but within it.
However, as straightforward as this analysis is, it is based on only three events. Normally, in a paper one would never consider presenting a statistical analysis based on so few samples, because when sample sizes are very small the probability of a Type II error when testing the null hypothesis is very high [15], and model validation is impossible [16, 17]. It is interesting to note that the Hope-Simpson paper was not in fact peer-reviewed, but rather correspondence to the editors of Nature. Had the paper been peer-reviewed by experts in influenza and/or statistics, it likely would have been pointed out that (a) half of the purported pandemics never actually occurred, and (b) the sample sizes were far too small for general inference.
In 1978, two astronomers, Hoyle and Wickramasinghe, espoused a theory that many diseases hitherto assumed to be infectious were actually seeded into the population from extraterrestrial origin [18]. As a ‘test’ of this theory, they attempted to explain the patterns of spread of influenza in day schools local to their university. They claimed that the only plausible explanation for the patterns they observed was that influenza was spreading in the population not via contact between people in the population, but through viruses arriving from outer space [18]. They announced their work in a paper in a news publication, New Scientist [19], which is not peer-reviewed.
Hoyle and Wickramasinghe subsequently published a note in 1990 that claimed that the sunspot/pandemic link purported by Hope-Simpson also occurred during the ‘1978–79’ pandemic, and that their theory of extraterrestrial influenza explained this phenomenon [20]. In reality however, the pandemic was in 1977, which was further from a solar maximum than 1978. Like the Hope-Simpson paper before it, the Hoyle and Wickramasinghe note was also a letter to the editors of Nature.
Once again, had the paper been peer-reviewed by experts, it likely would have been pointed out that they got the date of the 1977 pandemic wrong, and that a statistical analysis to support their hypothesis of the purported relationships of sunspot cycles to additional pandemics prior to 1900 was entirely lacking. Indeed, it was pointed out by Lyons and Murphy in a subsequent letter to Nature that cause must necessarily precede effect, and several of the pandemics discussed by Hoyle and Wickramasinghe preceded the solar maximum [21]. They also took issue with the definition of the pandemics used, as did von Alvensleben [22]. Von Alvensleben also pointed out that the pandemics listed by Hoyle and Wickramasinghe were in fact apparently randomly distributed within the periodic solar cycle.
Despite the questionable basis of these early, non peer-reviewed claims of an association between sunspots and influenza pandemics, it is now often talked about as an established ‘fact’ in the literature. Some, however, have put forward more biologically plausible explanations for the purported phenomena, including suggesting that vitamin D levels may depend on the variation in solar radiation during the sunspot cycle [23], and that the migration patterns of birds that spread the influenza may be sensitive to geomagnetic changes [24].
Sunspot data are readily available from the Royal Observatory of Belgium in Brussels (currently available at http://www.sidc.be/silso/datafiles, accessed September 2016). Using these data, other researchers have attempted statistical analyses to verify the purported association between influenza pandemics and sunspots. This analysis examines the work of researchers that claim to verify the sunspot/pandemic effect; Ertel, Tapping et al., and Yeung [25–27]. Two of the analyses claim that maxima in sunspot activity are associated with influenza pandemics [26, 27], while another claims that both maxima and minima in sunspot activity are associated with pandemics [25]. A brief synopsis of each analysis is given below, and each is described fully in Appendix A.
Before describing each analysis, however, some things should be noted about the general problems with these analyses, primarily related to issues of robustness to analysis assumptions, and problems with data mis-transcription from sources in the literature:
- If an analysis used a particular formulation of a ‘distance’ statistic to assess how far a particular year lies from a maximum or minimum in sunspot activity, the conclusion of the analysis should not depend on the exact formulation of distance statistic used, when other similar and equally valid distance statistics might be employed.
- Identifying pandemics, particularly prior to the 19th century, is a highly subjective process, and there is disagreement in the literature on the list of pandemics prior to the early 1800s. Analyses of the potential of a connection between sunspot number and influenza activity should be robust when using different, equally plausible lists of pandemics.
- Similarly, when using multiple citations to sources of lists of pandemic years, the analysis may involve assessing pandemic years by only taking years for which k out of the n sources agree; in which case, the analysis conclusions should be robust to different assumptions of k.
- There are two alternate specifications of sunspot activity, the Wolf (or ‘Zürich’, or ‘International’) and Group sunspot numbers; it has been noted in the literature that the latter is likely more accurate prior to the modern era, while the former is more accurate for characterising recent ongoing levels of sunspot activity [28–31]. Ertel, Tapping et al., and Yeung [25–27] all used the Wolf sunspot numbers, even though for the two latter analyses the Group sunspot numbers were also available. Analysis conclusions should be robust to different specifications of the sunspot activity.
- In general, analysis conclusions should be robust to changes in any of the arbitrary selections used in the analysis.
- Analyses should also be robust under alternate choices of the statistical analysis methodology used, particularly when a particular analysis method makes maximal use of the information in the data. Thus, an analysis that simply compared something like the mean of a ‘distance’ statistic for pandemic years to the average distance statistic for all years should be robust if a more powerful, non-parametric statistical test, such as the Kolmogorov–Smirnov or Anderson–Darling tests [32], is used to compare the shape of the two distributions from which the means are calculated. Two distributions, for instance, can have similar means, but very different shapes. And, particularly for small samples, one outlier in a distribution of just a few events may dramatically effect the mean, yet overall the distribution is consistent with being drawn from the larger distribution.
- Many of the different compilations of lists of past pandemics were actually derivative of the same historical sources. This is noted in Yeung [27], for example. The various references also cited each other frequently. Thus, lists of pandemics presented in the literature as being independent compilations, were not.
- Note here that the Ertel, Tapping et al., and Yeung [25–27] analyses all made transcription mistakes in the dates of influenza pandemics cited from the literature.
The following sections give brief synopses of the Ertel, Tapping et al., and Yeung [25–27] analyses, followed by a presentation of our own analysis of the available data. The robustness of the analysis to the assumption of various different, yet equally valid, ‘distance’ statistics, was assessed. For completeness, the analysis was performed using 10 different compiled lists of purported pandemics between 1700 and 1977, and also subsets of purported pandemics mutually agreed upon by k (where k goes from 1 to 10) of the reviews in refs [4–13] 1 (all of which were published after the 1977 pandemic, and cover the period from 1700 onwards). The pandemic year 2009 was added to the lists. Additionally, the robustness of the analysis to using the Wolf and Group sunspot numbers was assessed.
No statistically significant evidence that solar activity is related to influenza activity was found.
Ertel [25] analysis
In 1994, Ertel, a parapsychologist, performed an analysis claiming to verify that influenza pandemics occurred near both sunspot minima and maxima. He also published a later analysis claiming a link between sunspots and human creativity [36].
Using lists of influenza epidemics (many of which were not pandemics) between 1700 and 1985 from nine different sources in the literature [2, 12, 13, 19, 33, 37–40] and an encyclopaedia entry from 1970, Ertel arbitrarily defined a ‘pandemic’ to be an epidemic that at least three of the sources agreed upon. Ertel included in these sources several cited sources that were actually derivative of other cited sources (thus the 10 sources were not independent). Ertel also mis-transcribed data from several sources, and used some older references even when more up to date reviews were made available by some authors (for instance the list of epidemics in Beveridge et al. [38] was updated in Beveridge [10]).
To determine whether or not epidemics appeared to be clustered around the times of maxima and minima in sunspot activity, Ertel defined a metric based on the unsigned distance, D, in years of an epidemic from a sunspot maximum. He then transformed D into a new statistic, Q, which was −1 if D was the maximal possible distance between sunspot maxima, or +1 if it was at the minimum possible distance:(1)
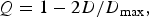
where D max is the maximum value of D during a solar cycle (where each solar cycle begins at the solar minimum).
While this statistic might, on the face of it, seem reasonable, it lacks sensitivity to whether or not an event occurs near a solar cycle minimum (the solar cycle is highly asymmetric in its periodicity, with maxima often occurring just a few years after a minimum, thus midway between two maxima usually does not correspond to the minimum, and the minimum in Q also thus does not generally correspond to the minimum in the solar cycle). Additionally, the Q statistic is not sensitive to whether the epidemic comes before or after the sunspot peak, and has only limited sensitivity to whether the epidemic is near a minimum in sunspot activity, despite the fact that Ertel was attempting to show that influenza epidemics occur near both maxima and minima in sunspot activity.
Cross-checking the analysis, as described in Appendix A, revealed that the results are highly sensitive to Ertel's choice of distance statistic and statistical analysis methodology. Correcting Ertel's mis-transcription of the data, and removing derivative lists of epidemics also negate Ertel's claims of significance.
Thus, largely because of the choice of distance measure and mis-transcriptions of data, Ertel concludes that sunspot activity is significantly associated with influenza activity.
In addition to these problems with the analysis, Ertel concluded that during the 1700s the influenza pandemics appeared to significantly occur around the sunspot minima, but after that there was no significant clustering. Ertel came up with an explanation for the decrease in significance by stating that it must have something to do with long-term changes in sunspot activity. This is an excellent example of ‘cherry-picking’ data, where it is claimed that the results testing the null hypothesis are significant… except where they aren't [41, 42].
Tapping et al. [26] analysis
Tapping et al. [26] performed an analysis where they examined the distance, in years, of influenza pandemics to the nearest sunspot maximum. The sunspot cycle periodicity is not constant and has varied since 1700 between 9 and 14 years. Tapping et al. [26] thus expressed the distance of pandemics to sunspot maxima as fractions of the period of the sunspot cycle at that point in time (i.e. as a phase), defined as(2)
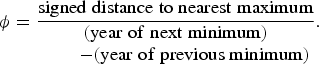
Using this metric, they attempted to determine if maxima in solar activity have been associated with subsequent increased incidence of influenza pandemics.
As described in Appendix A, the analysis of the data in the Tapping et al. [26] paper appears to have multiple issues, and their analysis results were not reproducible.
Yeung [27] analysis
Yeung [27] performed an analysis using Binomial confidence intervals to examine the statistical significance of the fraction of influenza pandemics occurring during years where the average number of sunspots was above the 60th percentile. The analysis was published in the journal Medical Hypotheses, which at the time was not peer-reviewed.
As described in Appendix A, there were several apparent typos or errors in the paper, and the results of the analysis were not robust to changes in the arbitrary cutoff in sunspot number. Indeed, the rather unusual choice of using the 60th percentile as a cutoff (rather than more obvious choices like perhaps the median, or the 10th or 90th percentiles) happens to have been in a relatively narrow range of selection values that ensured the best apparent statistical significance.
THIS ANALYSIS
Data
This analysis examined the data collected by several reviews of influenza pandemics from 1700 to 1977 [4–13], and added to these data the pandemic year of 2009. It should be noted that some of the reviewers listed only pandemics, while others listed both ‘serious’ outbreaks and pandemics. For consistency of comparison, of the latter only the ones designated by the reviewer as pandemics are tabulated. Table 1 summarizes the data for outbreaks labelled as pandemics. As noted in Table 1, many of the cited references have cited references in common (and indeed, cite each other). However, while the data are highly derivative, none of the lists are completely identical.
Table 1. Summary of influenza outbreaks from 1700 to 1977 labelled as pandemics, listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13]. The pandemic year of 2009 was also included in the data

3 Cites [12, 33–35, 43]. Has 1733 not 1732.
4 Cites [12, 13, 33–35, 38, 43, 44].
5 Cites [8, 10, 12, 13, 34, 35, 38, 43, 44].
7 Cites [10, 12, 13, 33–35, 38, 43]. Has 1799 not 1800.
9 Cites [12, 13, 33–35, 43, 44].
10 Cites [33, 35, 46]. Has 1782 not 1781.
12 Cites [33, 35, 38, 43, 44, 47].
Figure 1 shows the annual time series of Wolf and Group sunspot numbers by year [28–31] (available from the Royal Observatory of Belgium in Brussels, at http://www.sidc.be/silso/datafiles, accessed September 2016), with pandemic years indicated and coloured by number of reviewers agreeing that a pandemic occurred each particular year. For the period from 1995 onwards, the Group sunspot numbers are assumed to be the same as the Wolf numbers.

Fig. 1. Wolf and Group sunspots by year from 1700 to 2014. Overlaid is the timing of purported pandemics, as listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13], with the points coloured and sized relative to the number of reviewers agreeing on the date.
Analysis methods
For thoroughness, the data were analysed using several methods that have been used in the past. For all analysis methods, the results were examined for lists of pandemics agreed upon by at least k of the 10 reviews in Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13], where k goes from 1 to 10.
All analyses were repeated using the Wolf and Group sunspot numbers.
To begin, the fraction of pandemic years that came within ±1 year of maxima in sunspot activity were compared with the fraction for all years between 1700 and 2014. This was also done for the fraction of pandemic years that came within ±1 year of minima in sunspot activity, and also for either maxima or minima.
For pandemic years, the distribution of a temporal distance statistic for pandemic years to the nearest year of sunspot maxima was compared with the distribution for all years between 1700 and 2014. Two different statistics were explored:
- 1. The Q statistic used in the Ertel analysis [25], shown in Equation (1).
- 2. The ϕ statistic used in the Tapping et al. analysis [26], shown in Equation (2).
Finally, the distribution of sunspot numbers for pandemic years was compared with the distribution for all years, similar to the analysis of Yeung [27].
Statistical methods
The analysis of potential relationships between the timing of pandemic influenza epidemics and sunspot cycles presents several difficulties that appear to be under-appreciated in the literature.
To begin with, the analysis inherently involves small sample sizes. Influenza pandemics are relatively rare, and less than two dozen pandemics between 1700 and 2009 have been purported. In this analysis, when comparing the observed number, k, of n pandemics satisfying some selection criteria (like being within ±1 year of a solar sunspot maximum, for instance) to the expected fraction, p, the Binomial probability was assessed of observing by mere random chance at least k out of n, given p.
In many cases, one wishes to assess whether or not two distributions appear to be drawn from the same underlying distribution, such as the distribution of a metric that assesses the temporal ‘distance’ between a pandemic year to the nearest year of a sunspot maximum or minimum. Any binning of data to try to compare distributions necessitates loss of information [48, 49], thus in this analysis, the non-parametric two-sample Kolmogorov–Smirnov test [50], and Anderson–Darling test [51] are applied to compare the shapes of two distributions. The K–S and A–D tests do not require arbitrary binning of the data, and thus are more statistically powerful than binned methods of distribution comparison. The K–S and A–D tests are similar, but the formulation of the K–S statistic tends to be more sensitive to differences in the central portion of distributions, whereas the A–D statistic tends to be more sensitive to differences in the tails [51].
However, the standard P-values assessing the significance of these test statistics are only reliable for continuous data [50]. The data were necessarily binned in integer years, rather than being continuous in time, thus any distance statistic to sunspot activity extrema derived from these data will also not be continuous, but rather have a set of discrete values. Thus bootstrapping procedure was applied to assess the significance of the K–S and A–D statistics [52, 53] when the data are discrete. If the first sample is much larger than the second, each of sizes M and N, respectively, One thousand samples of size N were bootstrapped from the first sample, and the K–S and A–D statistics comparing the first sample to the bootstrapped sample were calculated. The distribution of these test statistics formed the probability distribution of the test statistic under the null hypothesis that the second sample was drawn from the same distribution as the first. This probability distribution was then used to assess the P-value of obtaining a value at least as large as some observed value of the K–S (or A–D) statistic (larger values of the statistic indicated distributions that were more different).
The sunspot activity data were continuous, thus to compare the distribution of sunspot activity of pandemic years to the distribution for all years, the standard P-value assessments of the K–S and A–D tests were employed.
The analysis was conducted in the R statistical programming language, version 3.3.2 [54]. The R code and data associated with the analysis can be found at https://github.com/smtowers/sunspots_and_pandemics_analysis.
Results
The results of the analysis of pandemics listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13], and assessed using the Wolf and Group sunspot numbers, are shown in Fig. 2.

Fig. 2. The results of the analyses of pandemic data as listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13], assessed using the Wolf and Group sunspot numbers (top row and bottom row of plots, respectively). The plots show the P-values assessed by the analyses, vs. the minimum number of reviewers agreeing that an outbreak or pandemic occurred. The first plot in the top and bottom rows shows the Binomial probability of the observed fraction of outbreak years within ±1 year of a maximum in sunspot activity, given the expected fraction for all years (and similarly for the years within ±1 year of an extremum in sunspot activity). The plots in the second, third, and fourth columns, respectively, show the re-creation of the Ertel, Tapping et al., and Yeung analyses [25–27], respectively, with the use of the Kolmogorov–Smirnov and Anderson–Darling tests to assess significance.
In all cases, and for all methodologies used, no significant association was found between sunspot number and pandemic timing.
SUMMARY
This analysis examined several past analyses that purported to show a statistically significant connection between sunspot activity and the timing of influenza pandemics. In all cases, the analyses either had mis-transcriptions of the dates of influenza pandemics listed in the literature, and/or made mistakes in the statistical analyses, and/or the analyses were not robust to arbitrary assumptions made to select the data, or the metrics used to assess the relationship between sunspot activity and the timing of influenza pandemics. In all cases, correcting these issues resulted in concluding that no significant relationship is apparent.
It is notable that in recent years other analyses have claimed that sunspot cycles influence everything from breast cancer incidence, to hip fractures, blood pressure changes, cardiac problems, plague, and cholera [55–58]. In addition to general poor statistical methodology, the problem with many such analyses is that some researchers search among a wide array of datasets for apparent statistically significant effects, publishing when they finally find them; a practice pejoratively known as ‘P-value fishing’ or ‘significance fishing’ [59]. By mere random chance, on average 5% of the time if one fishes among enough datasets, one will reject the null hypothesis with α = 0·05, even though the null hypothesis is actually true. 2
The analyses presented here are thus merely exemplars of wider problems, and reviewers can benefit from being aware of these issues.
1 Again, it must be noted that these references either cite each other, or have citations to early work in common (such as [33–35]).
2 Notably, the author has not come across any published analyses that show no significant relationship between sunspots and health phenomena, likely due to the ‘file drawer’ effect where uninteresting or null results are simply not published [60, 61].
APPENDIX A
INTRODUCTION
The following sections examine in detail the analyses of Ertel, Tapping et al., and Yeung [25–27]. Each of the analyses used different methodologies, and each purported to find statistically significant evidence that sunspot activity is related to the timing of influenza pandemics.
As will be described below, amongst other issues, all three analyses made mistakes in transcription of lists of pandemic years from the literature and/or in their calculations. All of the analyses were not robust to changes in the arbitrary assumptions made.
For reference when discussing these analysis, the data collected by several reviews of influenza pandemics from 1700 to 1977 have been compiled [4–13]. Subsets of these reviews (plus reviews that were entirely derivative of these) were used by the Ertel, Tapping et al., and Yeung [25–27] analyses. Table 2 summarizes the data for outbreaks labelled as pandemics.
Table 2. Summary of influenza pandemics from 1700 to 1977, listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [4–13]. In this analysis, the pandemic year of 2009 is also included in the data

13 Cites [12, 33–35, 43]. Has 1733 not 1732.
14 Cites [13, 12, 33–35, 38, 43, 44].
15 Cites [8, 10, 12, 13, 34, 35, 38, 43, 44].
17 Cites [10, 12, 13, 33–35, 38, 43]. Has 1799 not 1800.
19 Cites [12, 13, 33–35, 43, 44].
20 Cites [33, 35, 46]. Has 1782 not 1781.
22 Cites [33, 35, 38, 43, 44, 47].
It should be noted that some of the reviewers in Table 2 listed only pandemics, while others listed both ‘serious’ outbreaks and pandemics. For consistency of comparison from reviewer to reviewer, of the latter only the ones designated by the reviewers as pandemics were tabulated. As noted in Table 2, many of the cited references have cited references in common (and indeed, cite each other). However, while the data are highly derivative, none of the lists are completely identical.
ERTEL [25] ANALYSIS
Overview
In 1994, Ertel, a parapsychologist, performed an analysis claiming to verify that influenza epidemics occurred near the times of both sunspot minima and maxima [25]. He also published a later analysis claiming a link between sunspots and human creativity [36].
Using the Wolf sunspot numbers, and lists of influenza epidemics (not pandemics) between 1700 and 1985 from 10 different sources in the literature [2, 12, 13, 20, 33, 37–39, 62, 63], Ertel arbitrarily defined a ‘pandemic’ to be an epidemic that at least three of the 10 sources agreed upon. The data, as presented in Ertel [25], are shown in Table 3.
Table 3. Re-creation of Table 1 of Ertel [25]. The data were taken from Assaad, Beveridge et al., Hoyle, Collier's Encyclopedia, Creighton, Hope-Simpson, Patterson, Pyle, Silverstein, and Tschijewsky [2, 12, 13, 20, 33, 37–39, 62, 63]. The */** before/after a year indicates years that Ertel [25] identified to be within ±1 year of a minimum/maximum in solar activity. However, note that there are several errors in the data transcription from the sources (see text for details), and several sources list both pandemics and outbreaks, not just pandemics. Correctly transcribed data for pandemics only are shown in Table 2

To determine whether or not epidemics appeared to be clustered around the times of maxima in sunspot activity, Ertel defined a metric based on the unsigned distance, D, in years of a pandemic from a maximum in sunspot activity. He then transformed D into a new statistic, Q, which was −1 if D was the maximal possible distance between sunspot activity maxima, or +1 if it was at the minimum possible distance:(3)
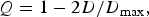
where D max is the maximum value of D during a solar cycle (where each solar cycle begins at a minimum in sunspot activity). While this statistic might, on the face of it, seem somewhat reasonable, it lacks sensitivity to whether or not an event occurs near a solar cycle minimum (the solar cycle is highly asymmetric in its periodicity, with maxima often occurring just a few years after a minimum, thus midway between two maxima usually does not correspond to the minimum, and the minimum in Q also thus does not generally correspond to the minimum in the solar cycle). The resulting statistic used in Ertel [25] thus was not sensitive to whether the pandemic came before or after the sunspot peak, and had only limited sensitivity to whether the pandemic was near a minimum in sunspot activity. This, despite the fact that the analysis was attempting to show that influenza pandemics occurred near both maxima and minima in sunspot activity.
Ertel took the average value of Q,
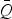
, for all pandemic years, and then used bootstrap methods to assess the probability of observing at least that value of
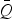
(note that a high value of
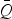
would indicate that pandemics were more likely to occur close to times of maxima in solar activity).
Re-creation of the analysis, as presented in the paper
In the caption of Table 1 in his paper, Ertel made the comment that he believed the fraction of the 286 years between 1700 and 1985 between ±1 year of a maximum or minimum in sunspot activity was 0·357 (i.e. he claimed 102 years were within 1 year of an extrema in activity). However, there were 51 extrema in sunspot activity during that period, thus the total number of years within ±1 year of an extrema in activity was 154 (1985 was 1 year before a minimum in solar activity in 1986), yielding an actual fraction of 0·538.
Note that Ertel mistakenly identified the year 1803 as not being close to an extrema in sunspot activity, but in reality it was within 1 year of a maxima. There were several errors in the data Ertel presents in the paper, as described below. However, taking the pandemic years presented in the paper at face value, 21 out of the 25 years were within 1 year of an extrema in sunspot activity, in agreement with the result quoted in the paper. The resulting average value of Q was
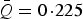
, in slight disagreement with the value presented in the paper of
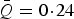
. Additionally this analysis found, using Ertel's bootstrapping method, that the probability of observing
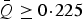
by mere random chance was P = 0·02, which is less impressive in its significance than the P = 0·005 quoted in the paper.
In addition, rather than just examining the mean of Q (which is based on a small sample size in this case), there are more statistically powerful non-parametric statistical tests, such as the Kolmogorov–Smirnov (K–S) and Anderson–Darling (A–D) tests [32, 50, 51], that compare two distributions and calculate the probability of observing the two, under the null hypothesis that the two samples were drawn from the same distribution. The K–S and A–D tests are similar, but the formulation of the K–S statistic tends to be more sensitive to differences in the central portion of distributions, whereas the A–D statistic tends to be more sensitive to differences in the tails [51]. When the K–S test was applied, comparing the Q of the pandemic years listed in Ertel [25] to the value of Q for all years between 1700 and 1985, a P-value of P = 0·10 was obtained. Applying the A–D test yielded a P-value of P = 0·09.
Thus, even with the erroneous data used as the basis for the original analysis, the claims of significance were not upheld when more statistically powerful tests of significance were used.
Corrections to the data
The author was able to locate and examine eight of the 10 references used in Ertel [25]. Of these eight, several were highly, or completely, derivative. For instance, Ertel's reference (12) was a paper by Assaad et al. [37] that cited Ertel's reference (7), Beveridge et al. [38]. In fact, the pandemics listed by Assaad et al. [37] were identical to the ‘probable’ pandemics listed by Beveridge et al. [38]. This was thus not an independent reference. Similarly, reference (15) in Ertel [25] was a book by Silverstein [39] that cited Beveridge et al. [38] as a reference, and the years listed by Silverstein in Table 1 of Ertel [25] were identical to the years listed by Beveridge et al. [38], thus this was also not an independent reference.
Ertel [25] listed the years indicated by Beveridge et al. [38] to be ‘possible’ or ‘probable’ pandemics, but inexplicably left out the years 1729, 1732, 1742, 1900, 1918, 1946, 1957, 1968, and 1977 listed by Beveridge et al. [38], and added the year 1800, which was actually noted to be 1802 in Beveridge et al. [38]. In the derivative Assaad et al. [37] data, Ertel included the ‘probable’ pandemic years listed by Beveridge et al. [38], but mis-transcribed 1977 as 1979.
Reference (6) in Ertel [25] was the paper by Hope-Simpson [2]; Ertel [25] mis-transcribed the 1977 pandemic year noted by Hope-Simpson as 1978. The Hope-Simpson paper additionally only listed pandemics from 1918 on wards. For proper assessment of source agreement on epidemic years, the sources should cover the same time period, and also use similar criteria in selecting ‘pandemic’ years. In the case of the data presented by Ertel [25], some of the sources listed epidemic years, and others, like Hope-Simpson [2], only listed pandemic years.
Reference (14) in Ertel [25] was a reference to the 1970 version of Collier's Encyclopedia, which the author could also not locate. Referencing encyclopaedic entries rather than the references cited within is a questionable, and the outbreak years listed in Collier's were certainly derivative of the other sources listed by Ertel [25].
Reference (16) in Ertel [25] was a paper the author could not locate, by Tschijewsky [63]. However, note the epidemics listed by Tschijewsky [63] were virtually identical to those listed by Creighton [33], which was Reference (10) in Ertel [25], with the addition of 1918.
Removed from consideration in the analysis were thus Assaad (identical to Beveridge et al. [38]), Creighton [33] (later sources either cited Creighton, or cited sources that cited Creighton), Silverstein (derived from Beveridge and Beveridge et al. [10, 38]), Tschijewsky (derived from Creighton), and the reference to Collier's Encyclopedia.
Ertel [25] also used some older references, even though more up to date reviews by some authors were available in at the time he wrote his paper (for instance, the 1977 list of pandemics in ref. [38] was updated in 1991 in [10], and the 1971 list in ref. [40] was updated in 1979 in [45]).
The correct data, for pandemics only (not an arbitrary mixture of epidemics and pandemics, as listed by Ertel) are included in the data sources shown in Table 2.
Use of corrected data, alternate sunspot number compilations, and alternate distance statistics
As described in the main text of this paper, the corrected data in Table 2 did not yield statistically significant evidence of a relationship between sunspot activity and the timing of pandemics, for either Ertel's Q statistic, or other equally valid analysis methods, and when using either the Wolf or Group sunspot numbers.
Summary
The data in Ertel [25] had many mis-transcriptions from the literature, and included a mixture of lists of influenza pandemics and outbreaks, even though the paper purported to examine only pandemics. However, taking the data in Ertel [25] as originally presented, this analysis largely verified the results presented in the paper, except the P-value was P = 0·02, not P = 0·005 as claimed, but the more powerful non-parametric K–S and A–D tests found no statistically significant difference between the distribution of Q for pandemic years compared with other years.
When the mis-transcribed data in Ertel [25] were corrected and several derivative sources were removed, this analysis found no statistically significant difference between the distribution of Q for pandemic years compared with other years.
TAPPING ET AL. [26] ANALYSIS
Tapping et al. [26] performed an analysis where they examined the distance, in years, of influenza pandemics to the nearest sunspot maximum. The sunspot cycle periodicity is not constant and has varied since 1700 between 9 and 14 years. Tapping et al. [26] thus express the distance of pandemics to sunspot maxima as fractions of the period of the sunspot cycle at that point in time (i.e.; as a phase). Explicitly, they define this as(4)

Using this metric, they attempted to determine if maxima in solar activity have been associated with subsequent increased incidence of influenza pandemics.
They binned these phases into five equally sized bins between –0·5 and +0·5. Note, however, that |ϕ| can be greater than 0·5 because a maximum in sunspot activity does not, in general, fall equidistant between two minima in sunspot activity. In fact, since 1700 the average duration between a minimum in sunspot activity to the next maximum is generally around 2 years shorter than the average duration between a maximum and the next minimum. Because of this, not only can |ϕ| > 0.5, but also ϕ is not uniformly distributed. Tapping et al. [26] did not mention that they were aware of this, and indeed, in their analysis, they assumed that ϕ should be uniformly distributed between –0·5 and +0·5. For the pandemic years that they examined, it happens that |ϕ| < 0.5 for all of them. They did not show the distribution of ϕ for non-pandemic years.
Using a Monte Carlo method that assumed these fractions were continuously and uniformly distributed between −0·5 and 0·5 (they were not), they then assessed the probability of observing the number of events in the two bins between −0·1 and +0·3, and concluded that significant effects were evident.
Re-creation of the analysis, as presented in the paper
The data in the Tapping et al. [26] were derived from Garrett and Potter [8, 9]. However, even though Tapping et al. [26] ostensibly examined only pandemics in their analysis, they included several years from both sources of data that were clearly labelled by the authors as not being apparent pandemics.
The data given in the Tapping et al. [26] paper are shown in Table 4. Shown in red are the years incorrectly transcribed as being listed as pandemics by the sources. In addition, Tapping et al. [26] make several apparent mistakes in their calculation of ϕ, as noted in Table 4. Note that these mistakes were apparently carried over into their histograms of the data shown in their paper.
Table 4. Re-creation of Table 1 in Tapping et al. [26], showing the years they considered as pandemic years in their analysis. In several cases, shown in blue, outbreaks clearly designated by the source as not being a pandemic year were included in the data. In addition, in the several instances indicated in red, the phase, ϕ, was incorrectly calculated

23 Is actually −0.42, not +0.42.
24 Is actually 0.00, not +0.10.
25 Garrett (1994) lists 1836, not 1837.
26 Because the year should be 1836, =0.00, not −0.10.
27 Should be −0.08, not −0.07.
28 Potter [8] states the pandemic began in 1898.
29 Because the year should be transcribed as 1898, not 1900, = +0.42, not −0.50.
30 Should be −0.10, not +0.20.
31 Should be −0.10, not +0.20.
Using the correctly calculated phases, this analysis was unable to reproduce the results of the Tapping et al. [26] paper.
Use of corrected data, alternate sunspot number compilations, and alternate distance statistics
As described in the main text of this paper, the corrected data in Table 2 did not yield statistically significant evidence of a relationship between sunspot activity and the timing of pandemics, for either the ϕ statistic used by Tapping et al. [26], or other equally valid analysis methods, and when using either the Wolf or Group sunspot numbers.
Summary
Unfortunately, the data, as presented in the Tapping et al. [26] paper, had multiple apparent errors in their calculation of their ϕ statistic, and they included several years in their analysis that were not listed as pandemic years by the sources.
When corrected data were used, as presented in Table 2, no statistically significant evidence of a relationship between sunspot activity and the timing of influenza pandemics was found.
YEUNG [27] ANALYSIS
Yeung [27] performed an analysis using Binomial confidence intervals to examine the statistical significance of the fraction of influenza pandemics occurring during years where the average number of sunspots is above the 60th percentile [27]. The analysis was published in the journal Medical Hypotheses, which at the time was not peer-reviewed.
This analysis is recreated below, and it is shown that there were several apparent typos or errors in the paper, and the results of the analysis were not robust to changes in the arbitrary cutoff in sunspot number, SSN. Indeed, the rather unusual choice of using the 60th percentile as a cutoff (rather than more obvious choices like perhaps the median, or the 10th or 90th percentiles) happens to have been in a relatively narrow range of selection values that ensured the best apparent statistical significance.
Again, as discussed below, to maximize the power of the analysis, the analysis of Yeung was refined to use un-binned methods, and no statistically significant evidence was found that sunspot number impacted the timing of influenza pandemics.
Re-creation of the analysis, as presented in the paper
The data used in the Yeung [27] analysis are shown in Table 5. Indicated in red in the table are data that were mis-transcribed from the original sources.
Table 5. Re-creation of Table 1 in Yeung [27], showing the years Yeung considered as pandemic years in the analysis. In several cases, indicated in red, the data are mis-transcribed from the original sources

32 Beveridge indicates 1729 was a pandemic year [10].
33 Pyle lists 1732 as a pandemic year [12].
34 Kilbourne lists 1782, not 1781.
35 Pyle [12] does not list 1800 as a pandemic year.
36 Potter [8] lists 1799 as a pandemic year.
37 Patterson [13] lists 1833, not 1831 as a pandemic year.
38 Kilbourne [11] lists 1833, not 1831 as a pandemic year.
39 Potter [8] lists 1847 as a pandemic year.
40 Potter [8] lists 1898, not 1899 as a pandemic year.
41 Cites Beveridge [10] for this [10].
Oddly, although Yeung [27] listed pandemics noted by five reviewers [8, 10, 11, 12, 13, 38], in the analysis he excluded the data from [13] without explanation.
The outbreaks agreed upon by Beveridge and Beveridge et al. [10, 38], Pyle [12], Kilbourne [11], and Potter [8] were, according to Yeung [27], 1729, 1781, 1830, 1889, 1918, 1957, and 1968. In reality, however, Pyle [12] did not list 1729 as a pandemic year, but rather 1732, and Kilbourne [11] listed 1833 as a pandemic year, not 1830. However, when the 7 years as presented were considered, 6 did indeed have a Wolf sunspot number greater than the arbitrary cut-off of 50, which was the upper 60th percentile, which yielded a P-value of P = 0·019, as presented in the paper.
However, SSN ⩾ 50 was the 60th percentile, which seems a somewhat odd choice. As shown in Fig. 3, it turns out that the choice of the 60th percentile as a cutoff yielded an almost maximal apparent significance in the result. Using a more standard percentile in the analysis, like the median, or 90th percentile, did not yield significant results. In addition, the use of the Group sunspot numbers in lieu of the Wolf sunspot numbers did not yield a significant result for any cutoff.

Fig. 3. Apparent significance of the results of the Yeung [27] analysis, as a function of the percentile value used to assess the cutoff in sunspot number, SSN. The result of Yeung [27] was obtained with an SSN percentile cutoff of 60% (0·6), which resulted in almost maximal apparent significance. Note that the Group sunspot numbers do not yield a significant result for any percentile used to assess the cutoff in SSN.
Summary
The Yeung [27] analysis made several mis-transcriptions of lists of pandemics in the literature, and arbitrarily chose to exclude one of the lists without explanation. Further, one of the selections used in the analysis was unusual in its choice, and was in a narrow range of values that achieved the best apparent significance; changing the selection to more standard values negated the claims of significance.
As noted in the text of the main paper, when corrected lists of pandemic years were used, along with more powerful un-binned non-parametric tests to compare the distribution of SSN for pandemic years to that of all years, no significant result was obtained with either the Wolf or Group sunspot numbers.
REFERENCES
1. Nicholls, H. Pandemic influenza: the inside story. PLoS Biology 2006; 4(2): e50.CrossRef | Google Scholar | PubMed
2. Hope-Simpson, RE. Sunspots and flu: a correlation. Nature 1978; 275: 86.CrossRef | Google Scholar
3. Hope-Simpson, RE. The Transmission of Epidemic Influenza. New York, USA: Springer Science & Business Media, 2013.Google Scholar | PubMed
4. Morens, DM, Taubenberger, JK. Pandemic influenza: certain uncertainties. Reviews in Medical Virology 2011; 21(5): 262–284.Google Scholar | PubMed
5. Mamelund, SE. Influenza, historical. Medicine 2008; 54: 361–371.Google Scholar
6. Lattanzi, M. Non-recent history of influenza pandemics, vaccines, and adjuvants. In: Giuseppe Del, Giudice, ed. Influenza Vaccines for the Future. New York, NY, USA: Springer, 2008, pp. 245–259.CrossRef | Google Scholar
7. Hampson, AW, Mackenzie, JS. The influenza viruses. Medical Journal of Australia 2006; 185(10): S39.Google Scholar | PubMed
8. Potter, CW. Chronicle of influenza pandemics. In: Nicholson, KG, Webster, RG, Hay, AJ, eds. Textbook of Influenza. Oxford: Blackwell Science, 1998, p. 3.Google Scholar
9. Garrett, L. The Coming Plague: Newly Emerging Diseases in A World Out of Balance. New York, USA: Macmillan, 1994.Google Scholar
10. Beveridge, WIB. The chronicle of influenza epidemics. In History and Philosophy of the Life Sciences. New York, NY, USA: Springer, 1991, pp. 223–234.Google Scholar
11. Kilbourne, ED. History of influenza. In: Kilbourne, Influenza. New York, USA: Springer, 1987, pp. 3–22.CrossRef | Google Scholar | PubMed
12. Pyle, GF. The Diffusion of Influenza: Patterns and Paradigms. Lanham, USA: Rowman & Littlefield, 1986.Google Scholar
13. Patterson, KD. Pandemic Influenza, 1700–1900: A Study in Historical Epidemiology. Rowman & Littlefield, Totowa, NJ, USA, 1986.Google Scholar
14. Clopper, CJ, Pearson, ES. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 1934; 404–413.CrossRef | Google Scholar
15. Suen, HK, Ary, D. Analyzing Quantitative Behavioral Observation Data. New York, USA: Psychology Press, 2014.Google Scholar
16. Chatfield, C. Model Uncertainty, data mining and statistical inference (with discussion). Journal of the Royal Statistical Society, series B 1995; 158: 419–466.CrossRef | Google Scholar
17. Casella, G, Berger, RL. Statistical Inference. Duxbury Press, Pacific Grove, CA, 2002, vol. 2.Google Scholar
18. Wickramasinghe, C, Wickramasinghe, K. A Journey with Fred Hoyle. The Search for Cosmic Life. Singapore: World Scientific, 2005, vol. 1.CrossRef | Google Scholar
19. Hoyle, F, Wickramasinghe, C. Influenza from space. New Scientist 1978; 79(1122): 946–948.Google Scholar
20. Hoyle, F, Wickramasinghe, NC. Sunspots and influenza. Nature 1990; 343(6256): 304.CrossRef | Google Scholar | PubMed
21. Lyons, D, Murphy, G. Influenza causing sunspots? Nature 1990; 344(6261): 10–10.CrossRef | Google Scholar | PubMed
22. Von Alvensleben, A. Influenza according to Hoyle. Nature 1990; 344: 374.CrossRef | Google Scholar
23. Hayes, DP. Influenza pandemics, solar activity cycles, and vitamin d. Medical Hypotheses 2010; 74(5): 831–834.CrossRef | Google Scholar | PubMed
24. Fuhrmann, C. The effects of weather and climate on the seasonality of influenza: what we know and what we need to know. Geography Compass 2010; 4(7): 718–730.CrossRef | Google Scholar
25. Ertel, S. Influenza pandemics and sunspots—easing the controversy. Naturwissenschaften 1994; 81(7): 308–311.Google Scholar
26. Tapping, KF, Mathias, RG, Surkan, DL. Influenza pandemics and solar activity. Canadian Journal of Infectious Diseases 2001; 12: 61–62.Google Scholar
27. Yeung, JWK. A hypothesis: sunspot cycles may detect pandemic influenza a in 1700–2000 ad. Medical Hypotheses 2006; 67(5): 1016–1022.CrossRef | Google Scholar
28. Hoyt, DV, Schatten, KH. Group sunspot numbers: a new solar activity reconstruction. Solar Physics 1998; 181(2): 491–491.CrossRef | Google Scholar
29. Hathaway, DH, Wilson, RM, Reichmann, EJ. Group sunspot numbers: sunspot cycle characteristics. Solar Physics 2002; 211(1–2): 357–370.CrossRef | Google Scholar
30. Vaquero, JM, Gallego, MC. Sunspot numbers can detect pandemic influenza a: the use of different sunspot numbers. Medical Hypotheses 2007; 68(5): 1189–1190.CrossRef | Google Scholar
31. Clette, F, et al. Revisiting the sunspot number. In: Balogh, A, Hudson, H, Petrovay, K, von Steiger, R, eds. The Solar Activity Cycle. New York, USA: Springer Publishing, 2015, pp. 35–103.Google Scholar
32. Richardson, A. Nonparametric statistics for non-statisticians: a step-by-step approach by gregory w. Corder, dale i. Foreman. International Statistical Review 2010; 78(3): 451–452.CrossRef | Google Scholar
33. Creighton, C. A History of Epidemics in Britain. Cambridge, UK: Cambridge University Press, 1894, vol. 2.Google Scholar
34. Thompson, T, Thompson, ES. Influenza or Epidemic Catarrhal Fever: An Historical Survey of Past Epidemics in Great Britain From 1510 to 1890. London, UK: Percival, 1890.Google Scholar | PubMed
35. Hirsch, A. Handbook of Geographical and Historical Pathology. London, UK: New Sydenham Society, 1883, vol. 1.Google Scholar
36. Ertel, S. Bursts of creativity and aberrant sunspot cycles: hypothetical covariations. In: Nyborg, H, ed. The Scientific Study of Human Nature: Tribute to Hans J. Eysenck. Bingley, UK: Emerald Group Publishing, 1997, vol. 80, pp. 491–508.Google Scholar
37. Assaad, F, Bektimirov, T, Ljungars-Esteves, K. Influenza – world experience. In: Stuart-Harris, C, ed. The Molecular Virology and Epidemiology of Influenza. Academic Press, New York, 1984, pp. 5–15.Google Scholar
38. Beveridge, WIB et al. Influenza: The Last Great Plague. An Unfinished Story of Discovery. London, UK: Heinemann Educational Books Ltd., 1977.Google Scholar
39. Silverstein, AM. Pure Politics and Impure Science: The Swine flu Affair. Baltimore, USA: Johns Hopkins University Press, 1981.Google Scholar
40. Burnet, FM. Naturgeschichte der Infektionskrankheiten des Menschen. Frankfurt, GE: Fischer, 1971.Google Scholar
41. Dienes, Z. Bayesian versus orthodox statistics: which side are you on? Perspectives on Psychological Science 2011; 6(3): 274–290.CrossRef | Google Scholar
42. Morse, JM. ‘Cherry picking’: writing from thin data. Qualitative Health Research 2010; 20(1): 3.CrossRef | Google Scholar
43. Finkler, D. Influenza in twentieth century practice. In: Stedman, TL, ed. An International Encyclopaedia of Modern Medical Science. 1899, pp. 21–32.Google Scholar
44. Vaughan, WT. Influenza: an epidemiologic study. Number 1. American Journal of Hygiene 1921; 1–245.Google Scholar
45. Burnet, FM. Portraits of viruses: influenza virus a. Intervirology 1979; 11(4): 201–214.CrossRef | Google Scholar | PubMed
46. Thompson, T. Annals of Influenza or Epidemic Catarrhal Fever in Great Britain From 1510 to 1837. Sydenham Society, 1852, vol. 21.Google Scholar
47. Ripperger, A. Die Influenza. Lehmann. Norderstedt, GE: Hansebooks, 1892.Google Scholar
48. Pyle, D. Data Preparation for Data Mining. Baltimore, USA: Morgan Kaufmann, 1999, vol. 1.Google Scholar
49. Williams, M. How good are your fits? Unbinned multivariate goodness-of-fit tests in high energy physics. Journal of Instrumentation 2010; 5(9): P09004.CrossRef | Google Scholar
50. Pettitt, AN, Stephens, MA. The Kolmogorov–Smirnov goodness-of-fit statistic with discrete and grouped data. Technometrics 1977; 19(2): 205–210.CrossRef | Google Scholar
51. Scholz, FW, Stephens, MA. K-sample anderson–darling tests. Journal of the American Statistical Association 1987; 82(399): 918–924.Google Scholar
52. Romano, JP. A bootstrap revival of some nonparametric distance tests. Journal of the American Statistical Association 1988; 83(403): 698–708.CrossRef | Google Scholar
53. Præstgaard, JT. Permutation and bootstrap Kolmogorov–Smirnov tests for the equality of two distributions. Scandinavian Journal of Statistics 1995; 305–322.Google Scholar
54. R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria, 2013. ISBN 3-900051-07-0.Google Scholar | PubMed
55. Caniggia, M, Scala, C. Sunspots and hip fractures. Chronobiologia 1990; 18(1): 1–8.Google Scholar | PubMed
56. Juckett, DA, Rosenberg, B. Time series analysis supporting the hypothesis that enhanced cosmic radiation during germ cell formation can increase breast cancer mortality in germ cell cohorts. International Journal of Biometeorology 1997; 40(4): 206–222.CrossRef | Google Scholar | PubMed
57. Babayev, ES, et al. Potential effects of solar and geomagnetic variability on terrestrial biological systems. Advances in Solar and Solar-Terrestrial Physics, Research Signpost, Kerala, India, 2012, pp. 329–376.Google Scholar
58. Burns, JT. Cosmic Influences on Humans, Animals, and Plants: An Annotated Bibliography. Lanham, USA: Scarecrow Press, 1997.Google Scholar
59. Figdor, C. New scepticism about science. Philosophers’ Magazine 2013; 60: 51–56.CrossRef | Google Scholar
60. Rosenthal, R. The file drawer problem and tolerance for null results. Psychological Bulletin 1979; 86(3): 638.CrossRef | Google Scholar
61. Dickersin, K. The existence of publication bias and risk factors for its occurrence. JAMA 1990; 263(10): 1385–1389.CrossRef | Google Scholar | PubMed
62. Collier. Collier's Encyclopedia. New York, USA: Collier Educational Corporation, 1970.Google Scholar
63. Tschijewsky, A. Dtsch-Russ. Med. Z. 1927; 3.Google Scholar